PythonKeys

In mathematics, the floor function, also known as the integer part, yields the greatest integer less than or equal to a given real number x. It's less than or equal to x, regardless of whether the number is positive or negative

For example, the integer part of 3.14 is 3 and the integer part of -3.14 is -4

This can be confusing also because according to the most popular A.I., in python int(-3.14)-1 = -5 which is a regrettable mistake. In python int(-3.14)-1 returns -4.

In Python, the built-in function int() indeed deals with integers, but it doesn't specifically return the integer part of a number. This can be seen when applying it to negative numbers. For example, int(-3.14) yields -3, whereas the integer part of -3.14 is -4. While Python doesn't have a dedicated built-in function for extracting the integer part, libraries like NumPy provide additional tools to handle such tasks.

Here's how to extract the integer part. Note that the math.floor() function returns an object of type integer, whereas the numpy.floor() function returns an object of type numpy.float64.

import numpy as np
import math
a = -3.14
print(math.floor(a)) # returns -3
print(np.floor(a)) # returns -3
print(math.floor(a)==np.floor(a)) # returns true
print(type(np.floor(a))) # returns numpy.float64
print(type(math.floor(a))) # returns int
print(int(a)) # returns -4

Note that the math.floor() function returns an object of type integer, whereas the numpy.floor() function returns an object of type numpy.float64

If you want to reproduce the floor function without relying on libraries, it could be done like this:


def integer_part(x):
    if x>=0:
        i = int(x)
    elif x<0:
        i = int(x)-1
    print(i)

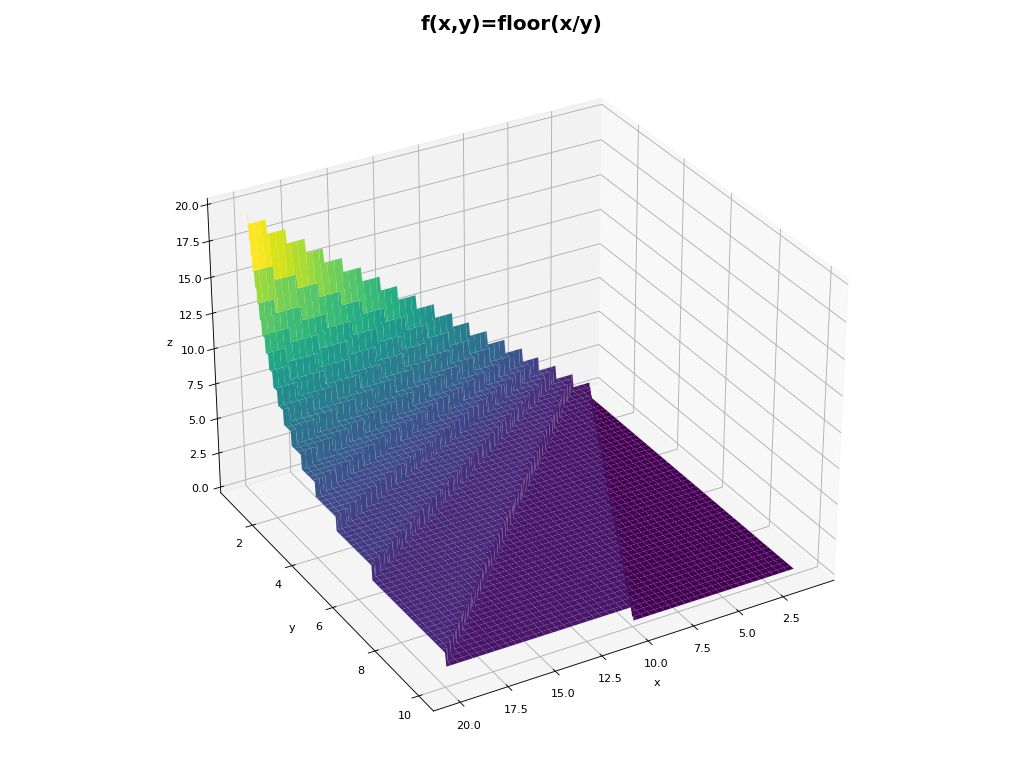
This is the function z = floor(x/y) in 3D using #Python and Matplotlib. Tt reveals surfaces defined by integer divisions and give insights into the behavior of discrete mathematical operations in continuous space.

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(1, 20, 300)
y = np.linspace(1, 10, 300)
X, Y = np.meshgrid(x, y)
Z = np.floor(X/Y)
fig,ax = plt.subplots(subplot_kw={'projection': '3d'})
fig.suptitle('f(x,y)=floor(x/y)',color="black",weight='bold',fontsize=18)
fig.subplots_adjust(hspace=0.5)
plt.tight_layout()
ax.azim=60
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.plot_surface(X, Y, Z, cmap=colormap)
plt.show()

see more articles

Integer Part