Solving a system of linear equations with Numpy
In this example, we will explore how to solve a system of n linear equations with n unknowns using NumPy. To understant this process, it's beneficial to have a basic understanding of linear algebra and matrix operations.
Let's consider solving a system of 4 linear equations with 4 unknowns (x, y, z, t):
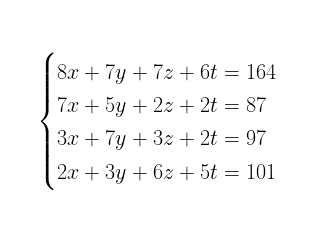
Before delving into the code, we express the system in matrix form as AX = B:

Subsequently, we represent these matrices as NumPy array objects in Python :
import numpy as np
A = np.array([[2,8,3,7],[5,2,7,8],[5,6,5,8],[4,3,6,2]])
B = np.array([110,125,133,94])Next, we verify that the determinant of matrix A is non-zero :
det_A = np.linalg.det(A)
print(det_A)
# prints -418.0
We then use the linalg.solve() function from the NumPy library :
S = np.linalg.solve(A,B)
print(S)
# prints : array([5., 6., 8., 4.])
That's it ! we have the solution. To validate our result, we can calculate the matrix product of A and this solution, using NumPy, and confirm that it matches the original matrix B :
print(A@S)
# prints : array([110, 125, 133, 94])
